討論頻寬與邏輯分析儀的時候,其實存在著相當多混淆不清之處。傳統上,邏輯分析儀向來被視為是一種純數位的量測工具,然而,隨著資料速率的提高以及上升時間的縮短,設計人員也必須要瞭解這種工具的類比特性。設計人員面臨的其中一個最大問題是:如何確保其驗證工具在這些較高的頻率下能夠正常運作?如果未能充分瞭解諸如設備的頻寬和負載等因素,可能會導致誤判的結果和擾亂整個系統。數位系統的設計人員必須要能夠信任所使用的邏輯分析儀,才能達到最快速的上市時間。隨著頻率持續地提高,邏輯分析儀的前端也必須與示波器的類比部份一樣,以謹慎小心的態度對待。
分析系統與驗證工具的頻寬時,工程師需要瞭解的主要考量有兩個,第一個是出現在其PCB上之數位信號中帶有的頻率成份,及其與邏輯分析儀頻寬的關連性,第二個是探棒的負載與這些頻率的交互作用為何。這兩個考量點最後都會牽涉到如何將數位信號轉換成類比量測指標的理論,以及如何運用這些指標來分析是否可以得到成功的量測結果。接下來的篇幅就要介紹可將數位信號轉換成類比量測指標的三種方法,分別是:上升時間對頻寬、切換速率(toggle rate)對頻寬以及脈衝寬度對頻寬等。一旦數位信號可以用頻寬來描述的時候,就可以輕易地分析出負載和邏輯分析儀的頻寬。
將上升時間轉換為頻寬
將數位信號的上升時間轉換為類比頻寬最常用的方法是使用一個單極的RC線路來模擬一個標準負載的響應,此線路會分別在時域和頻域中解出,得出以電阻值和電容值表示之上升時間和頻寬的經驗法則,再透過代入法將上升時間與頻寬的經驗法則聯立組合起來,如此一來就可以將電阻和電容的值捨掉,留下上升時間與頻寬之間的線性關係。(圖一)即是在此推導過程中用來模擬標準負載的RC線路。
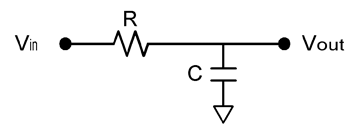
| 《圖一 同時在時域和頻域中解出RC線路可得出上升時間與頻寬之間的線性關係》 |
|
此推導過程的第一步是在時域中解出此線路,並假設此線路係用一個單位步進波形(u(t))來推動。一般的解法為:
由於上升時間的定義是Vout從10%轉變成90%所需的時間,因此可藉以解出此方程式,得到兩組不同的解答。第一組解答是由0伏特轉變成Vout的10%所需的時間,為了求出這個解答,我們將Vin設為1伏特,Vout設為0.1伏特。第二組解答也是透過相同的方法求出,但是將Vout設為0.9伏特。由於上升時間的定義是這兩個解答之間的時間差,因此最後只要將兩個時間相減,就可以得出RC線路之上升時間的經驗法則了。
此推導過程的第二個步驟是在頻域中解出同一個RC線路,此線路一般的解法為:
由於頻寬的定義為頻率響應的大小衰減了30%之處的頻率,因此可用以解出此表示式,得出一個經驗法則。
現在,已經得出以電阻值和電容值表示之上升時間和頻寬的一般表示式了,因此可將這兩個表示式聯立組合起來,得到單一個線性關係,此新的表示式可在數位信號的上升時間與該信號上升時間所帶有的頻率成份之間進行快速的轉換。
將切換速率轉換為頻寬
信號的數位切換速率可以透過傅立葉轉換轉為頻率的表示式。在傅立葉分析中,有一組可以依照不同的應用來調整的基本轉換式。在傅立葉表示式中,一個週期性的信號在時域中會以一連串出現在想要週期的脈衝信號來表示,這種表示式稱為Shaw函數(III(t)),轉換到頻域中則是另一個Shaw函數(III(s))。時域和頻域之間的大小調整是透過近似定理(Similarity Theorem)來達成的,該定理呈現出兩個域之間的反向關係(也就是時域中靠得較近的脈衝信號在頻域中會得出隔得較開的脈衝信號)。
數位系統中常用的一個經驗法則是系統的頻寬必須要能擷取到數位脈衝串的第三次諧波才算足夠,如果將這個法則與Shaw函數關聯起來看的話,第三次諧波指的是頻域中的第三個脈衝信號。下圖就是這種轉換及其與經驗法則的關係。
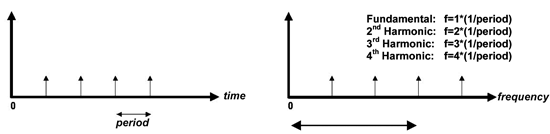
| 《圖二 時域中的週期性信號會用一連串以信號的週期間隔開的脈衝信號來表示,在頻域中則會被轉換為出現在(1/週期)的整數倍位置的一連串脈衝信號。》 |
|
量測一個週期性信號所需的總頻寬可以表示為:
將脈衝寬度轉換為頻寬
脈衝寬度也可以透過傅立葉轉換轉為頻率的表示式。在傅立葉表示式中,時域中的脈衝會以矩形函數(Π (t))來表示,當此函數轉換到頻域的時候,會得到sinc函數(sinc(s))。時域和頻域之間的大小調整同樣是利用近似定理來達成,該定理呈現出兩個域之間的反向關係(也就是時域中較窄的脈衝在頻域中會得出較寬的sinc波封)。
隨著頻率的提高,sinc函數會產生一連串的波封,sinc函數與零的交叉點會出現在sinc函數引數的整數倍位置,在此例中會出現在(1/寬度)的整數倍位置,(圖三)所示為時域的脈衝在頻域中的表示方式。
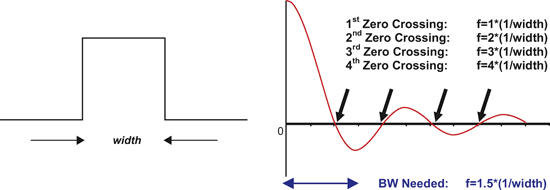
| 《圖三 將一個時域的脈衝信號轉換為頻域的sinc函數,此處的經驗法則為:系統的頻寬要能夠擷取到第二個sinc波封的一半位置才算足夠。》 |
|
如前面所提到過的,一個常用的經驗法則是系統需要具有足以擷取數位脈衝串的第三次諧波的頻寬,在傅立葉表示式中,數位脈衝串是以一個矩形函數與Shaw函數的迴旋運算結果來表示。在時域中,這樣做會產生一連串以資料串流的最高切換速率反覆出現的脈衝,此脈衝會以矩形函數來表示,而資料串流的週期性則以Shaw函數來表示,迴旋運算子會在時域中將這兩個函數聯立組合起來。在頻域中,矩形函數會轉換為sinc函數,Shaw函數會轉換為另一個Shaw函數,而迴旋運算子則會轉換為乘法運算。頻域中Shaw和sinc函數的相乘運算會產生Shaw脈衝被sinc函數的波封包住的結果。
對脈衝寬度比(duty cycle)為50%的脈衝串而言,Shaw脈衝會在(1/週期)每個整數倍的位置出現,sinc函數的波封會在(1/寬度)的每個整數倍位置與零交叉,因此會在這些頻率上將Shaw脈衝抵銷掉,剩下來的是Shaw脈衝在(1/週期)的每個奇數倍位置的值。第一個奇數的脈衝值稱為基本頻率(fundamental frequency),其它的奇數脈衝值則稱為諧波。如前所述,系統需要具有足以擷取數位脈衝串的第三次諧波之頻寬,在剛剛提到的這個特殊例子中,這會出現在第二個sinc波封的中間,隨著脈衝寬度變窄,這樣的頻寬是足夠的假設也必須跟著擴充才會夠用。現在可以改說:系統需要具有足以擷取到第二個sinc波封的一半位置的頻寬,才能可靠地傳送相關的脈衝,這種關係式可以寫成:
評估邏輯分析儀所需的頻寬
邏輯分析儀會依照與示波器前端線路類似的方式來訂定其前端線路的頻寬規格,當需要確定邏輯分析儀是否具有足夠的效能,用於偵測特定數位信號的問題時,可以使用上面提到的幾種轉換方式來評估。最好的解釋方法就是舉例說明,假設一個系統數位信號的規格如下,這些規格的每一項都可以轉換為類比頻寬,因此邏輯分析儀需要具有足以應付最高類比頻率的頻寬。
評估邏輯分析儀探棒的負載
邏輯分析儀也會規定其不同探棒選項的負載,一般會以集總電容值和/或阻抗值相對於頻率的特性來表示。若要快速地分析出探棒的負載是否會擾亂整個系統,可以使用集總電容值來進行。考量探棒的負載時,其電容值開始對目標信號造成分流時的頻率必須要夠高,才不會影響到前面提到的三種指標參數。探棒的電容值會與系統的傳輸線阻抗(一般為50Ω)形成一個RC濾波器,其頻率響應為:
如果使用前一節中所舉的例子來說明的話,可以找出探棒能夠帶入系統、但不會造成嚴重惡化情形的最高電容值。在上面的例子中,系統的數位信號需有1.875GHz的頻寬,將這個值帶入上面的表示式中就能得出系統可以容忍的最高探棒電容值,此處計算的結果為3.4pF。
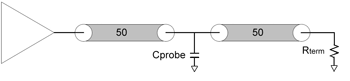
| 《圖四 邏輯分析儀探棒的電容性負載會與傳輸線的阻抗形成一個RC濾波器,為了不擾亂被探量的信號,探棒RC負載的3dB頻率必須大於數位脈衝串中會出現的最高類比頻率。》 |
|
結論
隨著數位系統的資料速率愈來愈高,工程師必須要瞭解所使用之驗證工具的極限。若能瞭解數位信號中出現的頻率成份,工程師就可以快速地評估出邏輯分析儀與分析儀探棒負載的效能。如果工程師事先能夠花一些時間來評估所使用之工具的效能,就可以提高量測成功的機率,並且大幅縮短啟動及驗證所需的時間。(作者為Agilent安捷倫科技Colorado Springs廠硬體設計工程師)
|
|
 |
過去幾十年來,數位設計人員一直仰賴邏輯分析儀做為驗證系統的主要工具。最近這幾年,時脈速率變得愈來愈快,使得設計人員必須要考量系統每個部份的信號完整性( signal integrity )問題,包括可測試性( testability )在內。 相關介紹請見「運用邏輯分析儀探量高速系統的考量」一文。 |
 |
專訪安捷倫行銷工程師巫介庭。你可在「數位時代的測儀之母邏輯分析儀」一文中得到進一步的介紹。 |
 |
設計差動式系統時,有許多錯誤的觀念需要先加以澄清,在開始探討差動式邏輯分析 儀探棒之前,有必要先釐清一些遭到誤解的觀念。在「差動式邏輯分析儀探量優劣評析」一文為你做了相關的評析。 |
|
|
 |
|
|
 |
Tektronix 發表 P6960 和 P6980 高密度無接頭探棒,兩款探棒使用新的 D-Max 探測技術,適用於 TLA700 系列邏輯分析儀。新的 D-Max 探測技術提供最高的通道密度和訊號完整性,遠優於同級的競爭產品,新探棒的探測面積比前一代小 61%。相關介紹請見「Tektronix推出新的無接頭邏輯分析儀探棒」一文。 |
 |
安捷倫科技 (Agilent Technologies) 日前宣佈,為使用邏輯分析儀除錯現場可 程式閘陣列 (FPGA) 提供業界第一個商用動態探頭應用程式。你可在「安捷倫為邏輯分析儀提供FPGA動態探頭應用程式」一文中得到進一步的介紹。 |
 |
電腦與通訊測試及量測設備廠商太克科技 (Tektronix) ,日前宣佈數位訊 號完整性測試用旗艦平台的重大性能進展。在「Tektronix推出頂級邏輯分析儀平台」一文為你做了相關的評析。 |
|
|
 |

