對於濾波器設計工程師們來說，如何設計窄通頻(Narrow Passbands)與轉換頻帶(Transition Bands)的部分，可說是最具挑戰性的任務之一，由於人們試圖將大量的資訊擠進範圍有限的頻譜當中，因此種種嚴苛的限制已經不能等到產品設計階段才討論，而必須向前移至濾波器規格確定階段，就必須將其納入考量。一般而言，這些限制往往提高了對高階濾波器(High Order Filter)的需求，所謂高階層數，指的是較長的長度，也就是要能提供較大的容量以儲存濾波器係數(Coefficeint)，並提供較高的執行速度以因應運算問題的處理；然而，事實上，就算極度高階濾波器的設計有可能達成，也是一件十分困難的工作。

本文將介紹如何以多頻取樣濾波器(Multirate Filters)的概念，在相當嚴苛的頻域限制下，完成有限脈衝響應濾波器(Finite Impulse Response Filters;FIR)的設計與實現。所謂多頻取樣濾波器是指：在濾波器的設計中，取樣資料輸入頻率可能有一次或一次以上的改變，且資料輸出頻率永遠維持與資料輸入頻率完全相同；而此種濾波器設計較一般標準的單一取樣頻率濾波器而言，能有效縮短濾波器長度與降低其所需的運算速度，提昇高階濾波器設計的可行性，否則，若以單一取樣頻率的概念來設計，恐怕絕非易事。

多頻取樣有限脈衝響應濾波器可運用許多標準的有限脈衝響應濾波器設計方法來設計；不過，在本文中，僅以Equiripple Design Technique(Remez)為例，為讀者詳細介紹。(註：此法試圖以濾波器頻率響應在衰減帶的起伏等量平均變化，達成濾波器設計的最佳化。)首先，本文將介紹如何以MATLAB完成濾波器設計，以Simulink完成動態模擬，以多頻取樣濾波器概念設計十分窄通頻的低通(Lowpass)、高通(Hightpass)、帶通(Bandpass)濾波器；其次，再以窄通頻濾波器設計的範例，延伸至非常寬通頻的濾波器設計。以下，即以一個窄通頻低通濾波器做為多頻取樣濾波器設計概念介紹的開場。

單頻取樣濾波器設計

假設將設計工程師們將設計能保留頻率低於70 Hz(赫茲)的訊號、濾除頻率高於80 Hz的訊號的一個低通濾波器(Lowpass Filter)(圖一)，且其取樣頻率為8 kHz，所以，若以取樣頻率的一半作為正規化的基準，則將此濾波器的拒絕頻率80 Hz正規化後，將為80/4000或0.02；此外，為了更詳細描述此有限脈衝響應濾波器，設計者還須明確指出其所能接受的最大通頻衰減值(Maximum Passband Attenuation)與最小拒頻衰減值(Minimum Stopband Sttenuation)，此例假設以0.15 dB或0.01 Linear為最大通頻衰減值，以80 dB或10-4 Linear為最小拒頻衰減值。

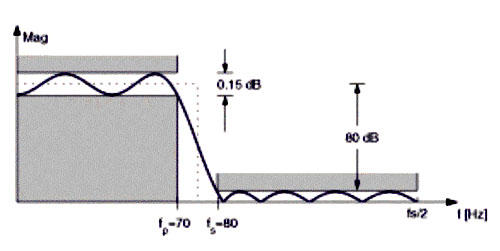
《圖一　An example of lowpass FIR filter design specifications》

接著，設計工程師們可以MATLAB及Signal Processing Toolbox中的功能函式remezord來預測其所需單頻取樣equiripple有限脈衝響應濾波器的階層數：

結果，階層數為2511(即濾波器係數=2512)的有限脈衝響應濾波器，這實在是一個相當長的濾波器！於是，此設計可以下列指令進行：

假設一個乘法及累積運算(MAC Operation)需要一對對稱的濾波器係數，則上樹脂濾波器所需的運算速度則為2512/12 MACs/sample*8000sample/sec，計算結果為10 million MACs/sec (每秒1千萬個乘法及累積運算)；本文將以此做為一個基準點，在接下來的介紹中，讀者便可以數據上的比較，體會到多頻取樣濾波器設計的優點。

多頻取樣窄通頻濾波器設計

讀者也許已經注意到：在上例單頻取樣設計中(圖二)，輸出訊號的頻寬相對於取樣頻率而言，顯得相當地窄；事實上，欲還原頻寬為80 Hz訊號的最小取樣頻率只需要160 Hz，也就是只要目前取樣頻率的160/8000，即1/50就可以了。這個事實給設計工程師們一個重要的啟示：設計工程師們可從每50個輸出訊號中取出一個訊號(取樣法：decimation；即每取50個樣本就移除49個樣本)，就能確保還原後的訊號不會失真。

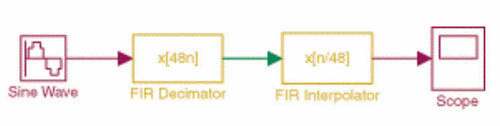
《圖二　Simulink model of a single-stage multirate FIR filter implementation of a lowpass narrowband filte》

所以，工程師們可採用一連串的取樣器(Decimator)來設計有限脈衝響應濾波器，此法的最佳例證即為所謂具取樣法概念的多相位有限脈衝響應濾波器(Polyphase FIR Decimation Filter)，因為其可有效以取樣因子(Decimation Factor)M降低其對於運算速度的需求；簡言之，每M個輸入樣本中，只取其中一個為樣本，其他的M-1個都將它們「丟卻」。因此，多相位有限脈衝響應取樣濾波器便可在不影響訊號還原準確性的情形下，以此取樣的方法，將連續M個輸入值化簡為一個輸入值，有效降低其所需的運算速度。

上述的取樣方法，的確是多頻取樣濾波器設計的精髓，不過，嚴格說來，它只完成了一半而已；接下來，設計工程師們還能採用另一個精髓來設計多頻取樣濾波器。一般而言，在多頻取樣的設計裡，工程師們都假設訊號輸出頻率等於其輸入頻率，因此，在訊號經過取樣之後，設計工程師們還必須在取樣後的多相位有限脈衝響應濾波器訊號結果裡，將數個訊號內插回去，以求得與原始輸入頻率相同的輸出頻率，這稱為內插法(Interpolation：Upsample Operation；即在每個樣本之後，插入L-1個值為0的訊號點)，可透過多相位有限脈衝響應濾波器(Polyphase FIR Interpolation Filter)來達成。與取樣器(Decimator)的原理相同，內插器(Interpolator)將可有效降低所需的運算速度至相當於原本的1/L；假設在訊號進入內插概念濾波器之前，每L個樣本都是非零的訊號點，則工程師們則可插入L-1個0，以略過0值的樣本，有效降低所需的運算速度，此即為一個最明顯的例子。

1.單階多頻取樣濾波器設計

截至目前為止，相信讀者對於如何以一連串的多相位有限脈衝響應濾波器的取樣與內插概念，設計出一個更有效率的多頻取樣濾波器，已經有了初步的認識。事實上，就單階多頻取樣濾波器(Single-stage Multirate Filter)而言，它並無法有效縮短濾波器的長度需求，不過，它確實能有效降低運算負擔；為了讓讀者有更深入的認識，首先就回到本文所討論的低通設計範例：設計工程師們可以選擇以48作為濾波器取樣群的樣本個數(依前例，最大取樣群樣本各數為8000/160=50，為了避免邊際值所引發的誤差，最好選擇較此最大值稍小一點的值作為取樣群樣本個數)。

於是，設計工程師們便可將其設計模型，以Simulink的區塊流程圖加以表現(圖二)：其中有限脈衝響應取樣器(FIR Decimator)與有限脈衝響應內插器(FIR Interpolator)，皆為DSP blockset工具箱中預先寫好的函式庫，只須以滑鼠拖曳，並輸入特定參數即可產生。而已知濾波器係數為2512(與單頻取樣有限脈衝響應濾波器設計中的值相同)，因此，其所需的運算速度可以下式求得：

2.多階多頻取樣濾波器設計

若設計工程師們對於單階多頻取樣所降低運算負荷的好處還不滿足，則可採用多階多頻取樣的濾波器設計(Multistage Multirate Filter Design)，因為，它能更進一步縮短濾波器的長度(即降低濾波器係數：Filter Coefficient)。舉例來說，工程師們可以不要以48作為取樣群組的樣本個數，而改以兩階段的取樣方式，則取樣群組的樣本個數可拆解成兩個，如：12和4、或是24和2、或者其他乘積為48的各種組合，如12*2*2的三階段取樣方法。本文則以12和4的組合，為讀者加以解說(圖三)。

《圖三　Simulink model of a two-stage multirate FIR filter implementation of a lowpass filter with narrow passband》

由於第一階段取樣的群組樣本個數為12，因此第一階濾波器的訊號必須在原先標準化取樣頻率的1/12(約為0.083)之前就切斷，才能避免訊號失真。讀到這裡，或許細心的讀者已發現到：0.083訊號切點較整體80 Hz設計的80/4000=0.02訊號切點的限制寬鬆許多，這就是第一階段取樣之所以能縮短濾波器長度的設計訣竅之一。

不過，這並不保證縮短濾波器長度的任務能夠達成，因為工程師們還必須考慮第二階段的取樣要如何幫忙完成整體的濾波器規格(70 Hz以下為通頻帶，80 Hz以上為拒頻帶；而現在的取樣頻率已是原先取樣頻率的1/12了)；當然，至少經過第一階段取樣後，第二階段取樣的限制就減輕多了，工程師們面對如何設計一個長度較短的兩階段濾波器，至少已經成功了一大半。然而，在此同時，工程師們必須謹記在心：由於其改採兩階段取樣方法，各階段濾波器頻率響應在衰減帶的起伏變化(Ripple)，都必須降為原來的一半，而此動作將加長整體的濾波器長度，因此，如何選擇最佳的取樣組合，以充分兼顧上述各種可能影響濾波器長度、運算負荷的因素，便是多階濾波器能否較單階濾波器更有效率的最大關鍵。

再回到本文所討論，以equiripple濾波器設計方法所實現的濾波器設計範例，若採多階多頻取樣的方法，則其第一階濾波器階層數為225，其計算指令如下：

所以，整體而言，此濾波器的係數為452(即225+1+225 +1)，較原先單階設計的濾波器係數2512大幅降低了許多。此外，此二階設計的取樣器運算負擔可以下式求得：

而同理可得，其內插器的運算負擔也是94 kMACs/sec，因此這個兩階段多頻取樣濾波器的整體運算負擔總和亦僅僅為188 kMACs/sec。

(表一)明確地比較「單頻取樣」、「單階多頻取樣」、「兩階段多頻取樣」設計在各方面的表現，讀者可強烈地感受到：只要設計工程師能慎選其取樣與內差的組合，兩階段多頻取樣濾波器(多階多頻取樣濾波器)，無論在濾波器長度上(較短)、或在運算負荷上(較小)的表現，都遠遠勝過其他兩種濾波器。

《表一　Comparison of single-and multirate filter implementations for an 80 Hz lowpass filter operating at an 8kHz input rate》

此外，值得一提的是，在多階多頻取樣濾波器設計原理中，設計工程師亦可融入框架基礎(Frame-based)的概念，以更進一步提昇其效率。(圖四)即為一個框架基礎、多階多頻取樣、窄通頻、低通濾波器設計的實例：在這個實例中，框架中的元素個數為48，所以取樣頻率已以框架大小表現出來，因此，如前述之12與4的取樣組合，在此例中，第一階段取樣後即留下48/12 = 4 個樣本。請注意：框架中的元素個數必須等於取樣組合的乘積(此例為48)，另外，無論是樣本基礎(Sample-based)或框架基礎的概念，皆可適用於本文所述的各種多頻取樣濾波器設計方法。

《圖四　Frame-based implementation of the multirate multistage narrow lowpass filter》

多頻取樣窄通頻的帶通與高通濾波器設計

1.多頻取樣窄通頻帶通濾波器設計

前述的窄通頻低通濾波器(Lowpass Filter With Very Narrow Passband)設計方法可延伸至帶通(Bandpass)與高通(Highpass)濾波器的設計，設計工程師們可採用九十度相位差模組化方法(Quadrature Modulation)，將多頻取樣的設計概念應用至帶通濾波器設計。基本上，工程師們可將所感興趣的帶通中央頻率模組化為基頻(頻率等於0)，以窄通頻低通濾波器處理後，再將模組拆解至原始的中央頻率，不過，由於九十度相位差模組化的過程需要複數訊號(相對於實數)進入低通濾波器，因此這些實質上與想像中的訊號處理，勢必增加帶通濾波器的運算負擔，而Simulink可完全支援這些必要的複數訊號，在(圖五)中以(c)表示。

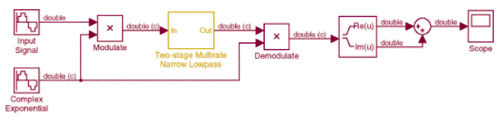
《圖五　Multistage multirate FIR filter implementation of a narrow bandpass filter》

(圖五)中可見，所有模組化(Modulation)與模組拆解(Demodulation)的動作都是指：乘上一個離散複數指數模組函式(Discrete Complex Exponential Modulation Function；m(n)；Fs samples/sec為取樣頻率，f為中央頻率)：

2.多頻取樣窄通頻高通濾波器設計

瞭解了多頻取樣窄通頻帶通濾波器的設計原理後，就能很快地將它延伸至多頻取樣窄通頻高通濾波器的設計上，事實上，只要將中央頻率設為取樣頻率的一半(Fs/2)，即可將一個窄通頻低通濾波器轉換成窄通頻高通濾波器，簡言之，這個模組化的函式可以下列式子表示：

相信設計工程師們看到上列函式，必定雀躍不已，因為這個模組化函式中，不再有複數了(因為cos(πn)=(-1)n，永遠在正負1兩個數中跳動)，這不但使得運算簡化許多，工程師們更可以免除將輸入訊號與m(n)相乘的動作，而直接將有限脈衝響應濾波器係數乘上+1、-1的連續性變化，即可將其頻帶模組化。因此，顯而易見地，窄通頻高通濾波器的設計原理事實上與窄通頻低通濾波器的設計原理相同，只不過是將其濾波器係數的正負號改變而已。[ 參考圖三、(圖四) ]

多頻取樣寬通頻濾波器設計

當設計工程師們已熟悉多頻取樣窄通頻低通、帶通、高通濾波器設計原理後，便可邁向多頻取樣「寬通頻」高通或低通濾波器的設計了。假設有一個窄通頻低通濾波器的轉換函式為L(z)，則相對於它的寬通頻高通濾波器轉換函式則為H(z)=1-L(z)，(其原理為：自一個全通(All Pass)濾波器響應中，扣除低通濾波器響應，即得寬通頻高通濾波器響應)。以時域概念來說，設計工程師們可從一個複製的延遲原始輸入訊號中，扣除多頻取樣低通濾波器的輸出訊號，就能完成寬通頻高通濾波器的模型，如(圖六)。

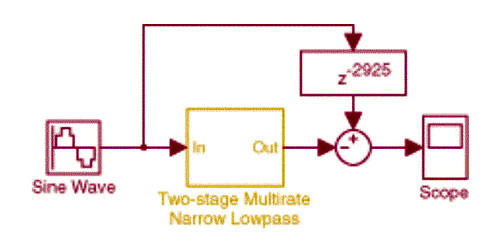
《圖六　Multistage multirate FIR filter implementation of a highpass filter with wide passband》

不過，設計工程師們要特別注意的是：延遲訊號的選擇，必須確認其延遲與多頻取樣濾波器群組延遲相同。舉例來說：單頻取樣有限脈衝響應濾波器的群組延遲，則為該濾波器長度的一半，而若就二階取樣低通濾波器而言，則其每一次取樣的群組延遲都必須依期原先的訊號輸入頻率而加以計算，也就是說，要以單頻取樣群組延遲的值，乘上之前的取樣群組樣本數，所以，回歸至先前討論的二階濾波器(已同時包含取樣器與內插器)，則其最終群組延遲樣本數N可計算如下：

同理可證，設計工程師們亦可以此原理，將一個窄通頻高通濾波器轉換為寬通頻低通濾波器。

結論

無論是極窄通頻、極寬通頻的濾波器設計，都可採用多階多頻取樣DSP濾波器設計技術來設計、實現、並提高其效率。MATLAB與Simulink提供設計工程師們一個最完整、最容易上手的設計、分析、模擬環境，讓工程師們面對複雜的系統時，也能遊刃有餘。(本文譯者目前任職於鈦思科技)