在许多情况下，量测质量和维持高取样率下能持续撷取数据的能力有关。在下文将以实例证明，数字器的内存深度可决定量测质量及精度。配备深内存的高速数字器具有强化时域及频域量测的能力。以下为以最大数字器取样率进行长时间数据撷取的应用。

严格来说，量测系统的功率是产品效能特征化、系统反应分析及缺陷分析的关键，搭配较深的内存可以改善时域及频域量测的信赖度及精确度。

时域的益处

当在进行时域分析时，了解所利用的一个既定取样周期及取样率所能撷取数据的最大时间是非常重要的。因为数据最终会由示波器转换到主计算机中的内存储存、显示及后续分析，示波器数据传输率受限于数据总线的带宽，如PCI。因为通常数据总线并没有足够的带宽去保持和高速示波器的全取样率，所以较深的内存是有必要的。藉由较深的内存，示波器可在较长的时间内以最大的速率撷取数据，所以其撷取时间区间便随之增加。撷取时间区间决定了能否撷取整个完整的讯号以作为分析之用。利用以下的公式（S/s＝取样数/秒）可计算撷取时间区间：

《公式一》

或就最大取样率而论（受限于示波器的规格）：

内建撷取内存＝记录于示波器内建内存的最大取样数

当选择取样率时必须考虑Nyquist理论。该理论说明一个讯号必须以至少二倍以上于其最高频率成分的取样率进行撷取，以精确地于示波器上重现其波形。低于其Nyquist频率的取样率会导致频谱区间中的高频部分失真。所谓失真即因太低的取样率而导致错误的低频讯号现在撷取的数据当中。(图一)显示一个25MHz的正弦波以30MHz取样频率的模拟数字转换器撷取所得到的结果。虚线表示25MHz频率的讯号因为带通效应，反而被错误地表示为一个5MHz的正弦波。为了避免失真，必须以大于50MHz的取样率来撷取这个25MHz的正弦波。这是说明在讯号量测上维持高取样率重要性的一个例子。

《图一 讯号失真》

在上文的公式中，可以以较低的取样率换取较长的取样区间，因为示波器内建的内存深度是固定的。较深的内存在维持高取样率的情况下可以撷取较长的时间。受限于示波器的内存深度，要去撷取封包化的波形是相当困难的，如影像讯号、磁盘读取频道及由许多成分组合而成的序列通讯讯号等。通常，唯一的方法可以去撷取整个讯号包络便是降低取样率。然而，一个较低的取样率会造成讯号质量下降及导致讯号包络中个别的高频讯号失真。举例来说，一个NTSC影像讯号包含每秒30张画面的画面速率，以及从30Hz到4.2MHz的频率成分。为了能够在100Msps的速率下撷取整张画面，需要一台可以撷取超过3.3MB笔数据的示波器。一台配备1MB内存的示波器将减少其取样率至约30Msps或以下。(图二)及(图三)表示在撷取一整张NTSC影像画面讯号时，减少取样率从100Msps到20Msps情况下，讯号衰减的结果。注意在水平线的颜色区域有部分讯号信息已经损失了。

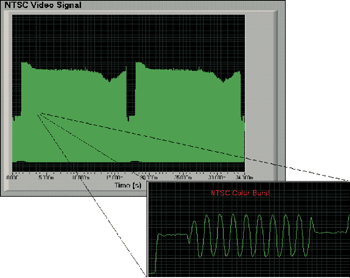
《图二 以100Msps撷取的单张NTSC影像画面》

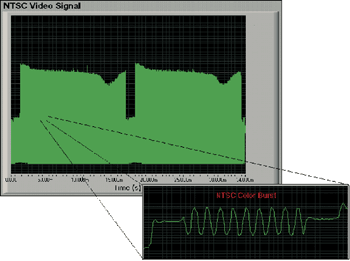
《图三 以20Msps撷取的单张NTSC影像画面》

(图四)则显示使用深的内建内存在一个延伸的时间区间去维持高取样率的好处。一台具有100Msps取样率及100KB内建内存的示波器可以支撑其最大的取样率仅维持1个毫秒。为了可以撷取2个毫秒的数据，这台示波器得减少其取样率至50Msps或甚至以下。一台具有100Msps取样率及32MB内建内存的示波器则可以支撑其最大的取样率为320个毫秒。

《图四 不同内存深度其取样率及撷取时间的关系》

频域的益处

高速示波器常用于撷取讯号以便于频域分析。当执行频域分析时，考虑失真效应是非常重要的。同样的，Nyquist理论陈述必须以至少二倍于讯号频率的取样率去撷取讯号，否则高频讯号的部分会失真，并且在通带上反而显示为较低频率的讯号。如果取样率大于二倍撷取讯号的最高频率，则频域分析才是有意义的。

频率分辨率

有几个FFT的算法用于计算离散傅立叶变换（DFT）。NI-Scope仪器驱动程序使用劈根实数FFT算法。这种劈根实数FFT算法计算n个点，这边的n是2的指数。如果撷取的点数并非2个指数倍数，则会在波形的尾部补0以增加数据点数至次高2的指数。虽然补0增加了数据点数，但其不影响FFT的结果。对n个点执行FFT运算造成有n/2个点落于正频域区。这些点定义一个介于DC及取样率一半间的频率范围。一旦点数已知，则可以使用下列公式计算FFT量测的频率分辨率。

《公式二》

依上述公式，当取样率减少及点数增加时，频率分辨率便会改善。减少取样率通常是个不讨喜的方法以改善分辨率，因为其减少了频率的展延或可用的带宽。藉由深的内建撷取内存，示波器可以在一个长时间内维持一个高取样率，等同于增加撷取的点数及改善频率分辨率。

举例来说，使用一台100KB内存及最高100Msps取样率的示波器时，可以从以上公式计算出其频率分辨率。取样率100Msps及取样点数设定为100,000点的频率分辨率为762.9Hz，其频率展开为DC到50MHz。100,000点会补0至131,072点，100Msps除以131,072得到频率分辨率为762.9Hz。

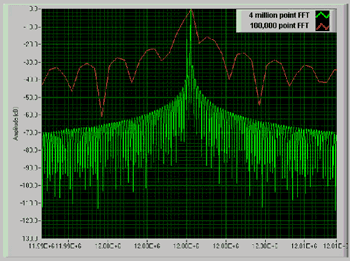
《图五 当撷取400万个点及10万个点分别的FFT频率分辨率》

(图五)显示当针对一个撷取的波形进行频率分析的最佳频率分辨率。在频率上非常靠近的二个讯号在有限的频率分辨率下会显示为同一根突峰。在图五中所撷取的讯号包含12.000000MHz及12.000180MHz的频率成分。一台内存为100KB及最大取样率100Msps的示波器无法解析这二个频率。即使降低取样率至二倍讯号带宽仍无法让仪器解析这二个讯号。因此可使用配备深内存示波器撷取400万点去解析这二个突峰。

频谱泄漏及窗口化

当使用离散傅立叶变换（DFT）或FFT去了解讯号的频率内容，这是假设已经撷取了一段周期性重复的波形。因为FFT会试着藉由复制有限的撷取点数去近似连续傅立叶变换（CFT）。如果撷取的数据并不包含一个整数周期，则无限区间中会有数个不连续点在有限撷取点的连接处。(图六)显示撷取非整数倍数周期的效应。

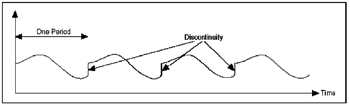
《图六 以非整数周期复制一个有限撷取所造成的不连续点》

这些人工的不连续点在FFT的频谱上为原始讯号中没有显现的高频成分。这些频率可能高出Nyquist频率许多，并且失真频率落于0及fs/2之间，这里的fs是指取样率。利用FFT所得到的频谱并不是原始讯号真实的频谱，而是一个失真的频谱。这显示在某一频率上的能量泄漏至另一频率上。这个现象称为频谱泄漏。频谱泄漏造成细长的频谱线展延成较宽的讯号。

(图七)显示一个由示波器所撷取的正弦波，及其对应的FFT强度（以分贝计量）。这个时域波形有一个整数周期（以此范例为2）， 所以是假设这个周期并不会造成不连续点。

《图七 未经频谱泄漏的FFT频谱》

(图八)是一个非整数倍时域波形频谱。这个讯号的周期延伸造成类似于(图六)中周期延伸的不连续点。注意能量是如何展延至一个较宽的频带中，所以介于FFT尖峰及邻近区域间的高度因而衰减了。这种由于能量的泄漏所造成的频谱失真称为频谱泄漏。频谱泄漏扭曲了能量由一个特定频率展延至邻近频带的量测结果。

《图八 经频谱泄漏的FFT频谱》

撷取讯号因非整数周期连接点处所造成的不连续点，而造成频谱泄漏的存在。此时可以利用名为窗口化的技术来减小这种因非整数周期的FFT运算所产生的效应。窗口化在每一个有限区间内减小在边界上不连续点的强度。

窗口化包含将波形乘上一段有限长度的窗口区间，而这个区间的振幅缓慢地变化至二端为0。因此当针对一段有限长度的数据执行FFT频谱分析时，可以使用窗口化技巧减小转换边缘的振幅改变，因此可以在无限区间内消除不连续点。通常有六种窗口化的种类可以选择，包含rectangular、Hanning、Hamming、Blackman、triangle及flat top。

(图九)显示当撷取一个非整数周期的讯号时，使用Hanning窗口化所带来的好处。第一张是从图八所撷取到的原始讯号，第二张图显示在经Hanning窗口化后的时域讯号，第三张图为经Hanning窗口化后讯号的FFT?频谱图。注意图九中经窗口化FFT和图八未经窗口化FFT的讯号相比，其频谱泄漏已下降许多。

《图九 Hanning窗口化的FFT频谱图》

如果欲观察的波形包含二个或以上的讯号，且这些讯号在频域上仅只有些微的差异，则频谱分辨率益显重要。在这个情况下，最好是选择一个主要波瓣较窄的窗口，如Hanning窗口。在既定的频率区间中，如果单一频率成分的强度、精度较其精确的位置来得重要，则选择一个波瓣较宽的窗口，如flat top窗口。Hanning是最常使用的一种窗口，因为它提供较佳的频率分辨率且可减少频谱泄漏。然而，考虑配备较深的内存以提升频率析度，flat top窗口反而提供比Hanning更多的好处。因为flat top窗口提供最佳的振幅精度及最陡峭的边缘波瓣。

动态范围

当进行频率量测时，了解其动态范围是相形重要的。所谓动态范围即量测系统所能处理的最高准位对最低准位的比值。此处解释在较大振幅讯号存在的情况下所能量取的最小讯号振幅有多少。

模拟数字转换器（ADC）的内部缺陷限制数字示波器的动态范围。在模拟前端及ADC的非线性反应造成共振扭曲，并且在FFT的频谱分析上显示为错误的讯号。

(图十)显示一个10MHz讯号的FFT频谱。注意出现在图上额外的频谱线并非原始10MHz讯号的任何部分。介于基本10MHz讯号及在30MHz最大失真频谱的动态范围约是46dB。

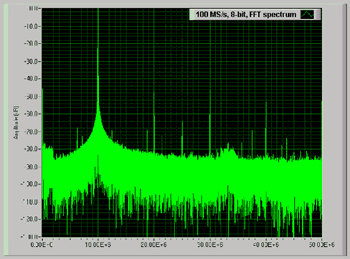
《图十 以100Msps撷取位于10MHz的FFT频谱图》

增加用以计算FFT频谱的取样数可以减少异步的噪声底线。每一个FFT频带显示在频带中所有的能量。增加更多的FFT取样数反而使每个频带的宽度变狭窄了。窄化每个频带的宽度会降低每个频带的所有噪声，并且降低噪声底线。这种噪声底线的改善是被证实的，因为增加FFT计算的点数并不会改变整个FFT频谱的所有能量。(图十一)显示增加撷取的点数从1024点至400万点的效应。

《图十一 400万点及1024点的FFT频谱图》

增加取样点数减少来自于异步噪声源的噪声底线，并且显示额外频谱线的发现是由于示波器内部的缺陷所造成。某些示波器包含有效位数（ENOB）或讯号对噪声比（SNR）等规格。所谓SNR即是所有讯号的功率对噪声功率的比值，常以分贝作为单位。SNR及ENOB能以下列公式计算求得。

《公式三》

平均化

可以针对示波器所撷取到的数据执行二种型态的平均化。时域平均化，也称为波形平均化，是在计算FFT前对时域的讯号作运算。而FFT平均化，相反地，是藉由撷取每个波形，分别计算FFT，然后对FFT频谱取其平均。每种平均的类型各有益处。

时域平均化是藉由针对多个触发点所得到的数据点取平均。这将衰减示波器的内部效应，如异步噪声效应，因此可以增加动态范围。噪声底线也依平均化的点数减低至一定的程度，但噪声底线的变异仍维持一个定值。这些效应如(图十二)所示，显示针对所撷取的讯号其动态范围取波形平均的益处。

《图十二 波形平均频谱》

FFT平均化是藉由撷取个别波形，分别计算FFT，然后对FFT频谱取平均。这个种类的平均化对减低噪声底线的变异是非常有效的。(图十三)显示FFT平均化的效应。

《图十三 FFT平均频谱》

延 伸 阅 读	PAC可提供工程师高级控制所需要的PC功能、实时分析或企业连接能力，同时保有PLC的可靠性。相关介绍请见「PAC进军自动化领域优势概论」一文。 数据记录是相当普及的量测应用，在多种领域中皆可见其身影。数据记录可让工程师测量不同的现象，从天气到工厂效能。你可在「PC-Based数据记录技术发展与现况」一文中得到进一步的介绍。 电信研究所已针对ATM高速网络进行关键组件之开发，目前已完成宽带虚拟路径交换机(BEX-VPX)、宽带数字器(BEX-AMX) 、ATM LAN SWITCH/HUB等之发展。在「中华民国国家信息基础建设之远景与蓝图」一文为你做了相关的评析。

市场动态	当与该公司精密的DC、RF和高速数字PXI仪器结合时，这些新模块非常适用于消费性电子商品、半导体、军事/航空电子设备。相关介绍请见「NI推出200MS/s PXI数字器和任意波形产生器」一文。 使用LabVIEW 7 Express，配合NI PCI-5911 100MHz可变动分辨率高速数字器，在有线电视机顶盒(set-top-box)上进行语音及影像的参数测试。你可在「亚旭计算机使用NI模块化仪器完成机顶盒自动化测试系统」一文中得到进一步的介绍。 现在工程师和科学家可以使用最新的USB标准─USB 2.0的高速度来控制GPIB仪器。在「NI推出可高速控制GPIB仪器的USB控制器」一文为你做了相关的评析。